ALGEBRA LINEAL
MATRICES
Una matriz es un conjunto ordenado en una estructura de filas y columnas. Los elementos de este conjunto pueden ser objetos matemáticos de muy variados tipos, aunque de forma particular, se trabajará exclusivamente con matrices formadas por números reales. Estas se denotan con corchetes o paréntesis.

En los siguientes dos vínculos encontrará explicaciones claras sobre el concepto general de matrices, tipos de matrices; suma, resta y multiplicación de matrices. Seleccione la forma como desea visualizar la información: En forma de presentación (vínculo izquierdo) o en forma de fichero pdf (vínculo derecho). Se abrirá una nueva ventana para la selección.
En los siguientes tres videos se describe el procedimiento para la suma y resta de dos matrices.
En los siguientes tres videos se describe el procedimiento para la multiplicación de dos matrices.
En los dos siguientes vínculos se encuentra un Taller de Ejercicios Resueltos y un Taller de Ejercicios propuestos para ser desarrollados por los estudiates.
TALLER DE EJECICIOS RESUELTOS
TALLER DE EJECICIOS PROPUESTOS
MATRIZ INVERSA
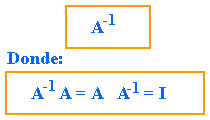
Dada una matriz A, ¿Podremos encontrar otra matriz B tal que A·B=B·A=I?
Esta matriz B existe aunque no siempre, de existir se le llama matriz inversa de A y se nota A-1. Para que exista la inversa de A, ésta tiene que ser cuadrada pues de lo contrario no se podría hacer el producto por la izquierda y por la derecha, luego cuando hablamos de matrices invertibles estamos hablando de matrices cuadradas.
En los siguientes dos vínculos encontrará explicaciones claras sobre el concepto general de matriz inversa, el cual será visto con más detalle posteriormente cuando estudiemos el tema de Solución de ecuaciones mediante el método de Gauss - Jordan.
Seleccione la forma como desea visualizar la información: En forma de presentación (vínculo izquierdo) o en forma de fichero pdf (vínculo derecho).
APLICACIONES DE MATRICES
Las matrices tienen diversas aplicaciones en la ingeniería civil por ejemplo en el cálculo estructural para analizar la capacidad de carga y el diseño de elementos; en ingeniería de tránsito para generar matrices de información en la planificación de transporte y aforos vehiculares; en topografía para realizar resúmenes de datos y cuadricular terrenos para curvas de nivel; en dibujo asistido por computadora en el software Autocad; en estática para resolver problemas de equilibrio en el espacio en 3D con operaciones vectoriales; en hidráulica para hacer referencias del estudio de la pérdida de energía por accesorios (circuito cerrado) y en el análisis, diseño y distribución de caudales para la población; en análisis numérico para resolver sistemas de ecuaciones lineales.
En los siguientes dos vínculos encontrará varios ejercicios con la aplicación de matrices en Ingeniería y Economía
Seleccione la forma como desea visualizar la información: En forma de presentación (vínculo izquierdo) o en forma de fichero pdf (vínculo derecho).
El el siguiente vínculo encontrará un taller de ejercicios resueltos sobre Aplicación de Matrices.
TALLER DE EJECICIOS RESUELTOS