FÍSICA MECÁNICA
MOVIMIENTO PERIÓDICO
Un movimiento armónico simple es el que describe una partícula sometida a una fuerza restauradora proporcional a su desplazamiento. Se genera entonces un movimiento periódico, es decir que se repite cada cierto intervalo de tiempo. No todos los movimientos periódicos son armónicos. Para que lo sean, la fuerza restauradora debe ser proporcional al desplazamiento.
El problema del oscilador armónico simple aparece con mucha frecuencia en Física, ya que una masa en equilibrio bajo la acción de cualquier fuerza conservativa, en el límite de movimientos pequeños, se comporta como un oscilador armónico simple.
El estudio del oscilador armónico constituye en Física un capítulo muy importante ya que son muchos los sistemas físicos oscilantes que se dan en la naturaleza y también muchos han sido producidos por el hombre.

MOVIMIENTO ARMÓNICO SIMPLE
Los movimientos periódicos ocurren en objetos que tienen un comportamiento cíclico. Un péndulo cuando se mueve, tiene un movimiento cíclico. Aquí un ciclo es un ir y regresar al mismo punto, pasando por todos los puntos de la trayectoria.
La Luna en su movimiento alrededor de la Tierra, da una vuelta completa en aproximadamente 28 días. Es un movimiento cíclico.
Para que esos movimientos sean periódicos debe ocurrir que en cada ciclo empleen el mismo tiempo.

Ejemplos de movimientos periódicos son el columpio, el péndulo, la Luna girando en torno a la Tierra, Un objeto colgando de un resorte, que se le ha sacado previamente del equilibrio.
-
Movimiento periódico. Un movimiento es periódico cuando a intervalos iguales de tiempo, todas las variables del movimiento (velocidad, aceleración, etc.) toman el mismo valor. Ej. el giro de la Tierra alrededor del Sol.
-
Movimiento oscilatorio. Es un movimiento periódico en el que la distancia del móvil al centro de oscilación pasa, alternativamente, por un valor máximo y otro mínimo. Por ej. un péndulo.
-
Movimiento vibratorio. Es un movimiento oscilatorio que tiene su origen en el punto medio y en cada vibración pasa por él. Las separaciones a ambos lados del centro se llaman amplitudes y son iguales. Por ej. una varilla sujeta por un extremo a la que damos un impulso en el otro. La varilla vibra.
-
Movimiento Armónico Simple (M.A.S.). Es un movimiento vibratorio, por lo tanto periódico y oscilatorio.
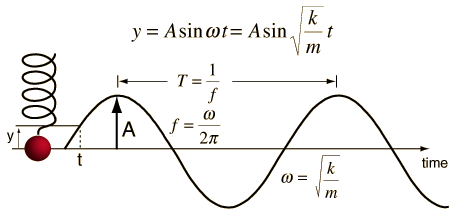
La ecuación que determina la posición es una función matemática seno o coseno, por eso se les llama funciones armónicas, y el movimiento descrito por estas funciones se llama movimiento armónico.
x = A sen(w t)
TIPOS DE MOVIMIENTOS EN LA NATURALEZA
Un cuerpo sujeto a un resorte

Frente a la perturbación de un cuerpo en equilibrio estable, la naturaleza responde con un movimiento que tiende a que el cuerpo vuelva a recuperar su posición de equilibrio. Este movimiento en su versión más sencilla se denomina “movimiento armónico simple” (m.a.s.).
Este tipo de movimientos se da continuamente en la naturaleza (movimiento de un resorte, el péndulo, movimiento de los átomos en la materia, etc.) y no solamente con cuerpos materiales sino también con valores de magnitudes (la presión del aire da lugar al sonido, los campos electromagnéticos dan lugar a la luz, etc.). Por ello es importante su estudio.
RELACIÓN ENTRE EL MOVIMIENTO CIRCULAR UNIFORME
Y EL MOVIMIENTO ARMÓNICO SIMPLE
Podemos imaginar un Movimiento Armónico Simple M.A.S. como una proyección de un Movimiento Circular Uniforme. El desfase nos indica la posición del cuerpo en el instante inicial.
Existe una relación directa entre el movimiento armónico simple y el movimiento circular: Un movimiento circular se proyecta como un movimiento armónico simple en su propio plano. Es por ello que a la hora de definir las magnitudes que representan el movimiento armónico simple conviene tener en mente la analogía con el movimiento circular.

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación
x = A sen (wt + j)

donde
A es la amplitud.
w la frecuencia angular o pulsación.
w t + j la fase.
j o jo la fase inicial.
Características de un M.A.S. son:
-
Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre +A y -A.
-
La función seno es periódica y se repite cada 2 PI, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2 PI, es decir, cuando transcurre un tiempo T tal que w(t+T)+j=w t+j+2 PI .
T = 2 PI/w
En los siguientes dos vínculos encontrará explicaciones claras sobre el Movimiento Armónico Simple MAS. Seleccione la forma como desea visualizar la información: En forma de presentación (vínculo izquierdo) o en forma de fichero pdf (vínculo derecho).
En los siguientes videos se presentan los conceptos básicos de Movimiento Armónico Simple
En los siguientes videos se presentan ejercicios resueltos sobre Movimiento Armónico Simple
SIMULADORES DE MOVIMIENTO ARMÓNICO SIMPLE
INTRODUCCIÓN AL MOVIMIENTO ARMONICO SIMPLE.
Permite visualizar el movimiento armónico simple MAS a partir del movimiento circular uniforme que realiza una particula.
El movimiento armónico simple interpretado como la proyección de un movimiento circular uniforme.
MOVIMIENTO ARMONICO SIMPLE DE UN RESORTE HORIZONTAL
Muestra gráficamente el comportamiento del desplazamiento en el eje x, la velociadad y la aceleración, para un resorte horizontal cuando es desplazado de su posición de equilibrio.
Igualmente muestra en forma gráfica el comportamiento de las eenergía potencial eslástica y cinética en función del desplazamiento de resorte de su posición de equilibrio.
MOVIMIENTO ARMONICO SIMPLE DE UN RESORTE VERTICAL
Muestra gráficamente el comportamiento del desplazamiento en el eje Y, la velociadad y la aceleración, para un resorte vertical cuando es desplazado de su posición de equilibrio.
Permite seleccionar la constante de elasticidad y la masa del resorte, y la amplitud máxima del movimiento en el eje y. Muestra el comportamiento grafico en función senosoidal y en vectores de las variables desplazamiento, velocidad y aceleració del movimiento.
COMPORTAMIENTO DE LA ENERGÍA DE UNA PARTICULA QUE DESCRIBE UN MOVIMIENTO ARMONICO SIMPLE
Muestra gráficamente el comportamiento del desplazamiento de las energías cinética y potenciasl de una particula que describe un Movimiento Armónico Simple.
Permite identificar claramente el valor de las energía cinética y potencial en cada uno de los instantes del movimiento armónico simple y determinar su comportamiento.
EL PÉNDULO
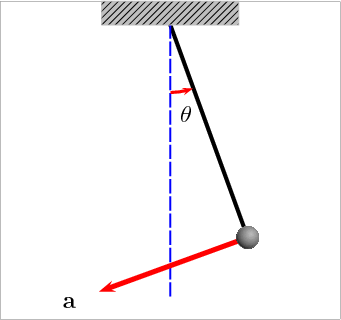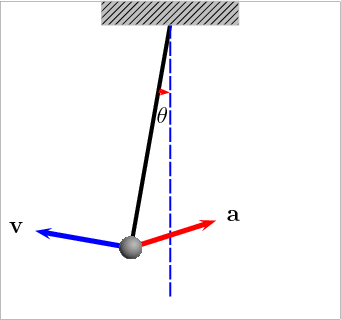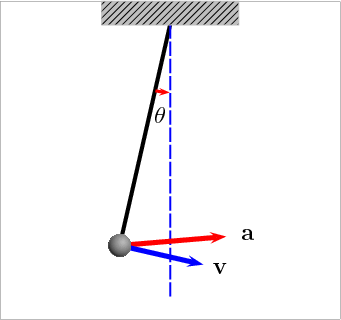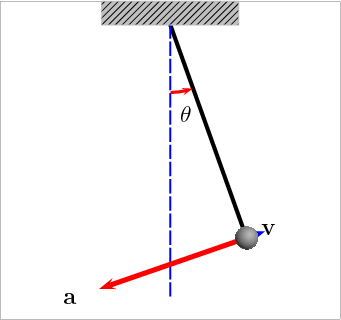
El péndulo (del lat. pendŭlus, pendiente) es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla, u otro dispositivo que sirve para medir el tiempo.
Existen muy variados tipos de péndulos que, atendiendo a su configuración y usos, reciben los nombres apropiados: péndulo simple, péndulo compuesto, péndulo cicloidal, doble péndulo, péndulo de Foucault, péndulo de Newton, péndulo balístico, péndulo de torsión, péndulo esférico, etcétera.
En los siguientes dos vínculos encontrará explicaciones claras sobre el PÉNDULO, la ecuación general que describe su comportamiento y ejercicios resueltos. Seleccione la forma como desea visualizar la información: En forma de presentación (vínculo izquierdo) o en forma de fichero pdf (vínculo derecho).
SIMULADORES DEL MOVIMIENTO DE UN PÉNDULO
MOVIMIENTO DE UN PÉNDULO IDEAL
Ilustra cómo varían la elongación, velocidad, aceleración tangencial, fuerza y energía durante la oscilación de un péndulo (se supone ausencia de rozamiento).
Se desprecia en los cálculos, la débil dependencia del período de oscilación con la amplitud (en el margen de amplitudes permitido en esta aplicación).
MOVIMIENTO DE UN PÉNDULO REAL
Permite determinar el periodo de un péndulo real pudiendo modificar su longitud, masa y angulo inicial. Se pueden comparar gráficamente el periodo de dos péndulos y evaluar la dependencia del péndulo de la longitud y el ángulo inicial.
Se pueden evaluar los resultados modificando la fricción del movimiento del péndulo.
MOVIMIENTO DE UN PÉNDULO SIMPLE
Se puede obtener el periodo del movimiento de un péndulo con base en su longitud, su masa y el ángulo inicial de elongación máxima.
El ángulo inicial debe ser menor o igual a 10 grados.
En los siguientes vínculos se encuentra un taller de ejercicios resueltos y un taller de ejercicios propuestos sobre Movimiento Armónico Simple y Péndulos
TALLER DE EJERCICIOS RESUELTOS MOVIMIENTO ARMÓNICO SIMPLE Y PÉNDULOS
TALLER DE EJERCICIOS PROPUESTOS MOVIMIENTO ARMÓNICO SIMPLE Y PÉNDULOS
SIMULADORES DE MOVIMIENTO ARMORGITUADO
MOVIMIENTO AMORTIGUADO DE UN RESORTE
La simulación muestra el comportamiento en el tiempo de la elongación o distancia x del resorte a su punto de equilibrio.
Se puede modificar el valor de la masa del objeto, la constante de elasticidad del resorte y el valor de b que corresponde a la constante de amortiguación del movimiento. Se observa como cambia la gráfica de x en función del tiempo al modificar el valor de b.
RESONANCIA EN UN MOVIMIENTO ARMÓNICO
Se disponde de un número de resortes que oscila a una frecuencia natural dada por la constante de elasticidad del resorte y su masa. Estos resortes oscilando se se situan sobre un manejador que oscila a una frecuencia dada.
La simulación permite modificar tanto la frecuencia de oscilación de los resortes (modificando la constante k y la masa del resorte), como la frecuencia de oscilación de manejador.
Se observa que cuando las dos frecuencias, la de oscilación del resorte y la del manejador, están cercanas; la amplitud del movimiento del resorte se incrementa notoriamente. Se evidencia claramente el fenómeno anterior, conocido como resonancia, cuando la frecuencia de uno de los resorte se hace igual a la frecuencia del manejador.
La simulación de la izquierda muestra como varia la elongación (X) en función del periodo del Movimiento y del ángulo de desfasaje inicial.
LEY DE HOOK
Muestra gráficamente la Fuerza que experimenta una masa conectada a un resorte horizontal en función de la constante de elasticidad del un resorte horizontal y del desplazamiento o elongación (distancia entre la posición de un punto en el resorte y la posición o centro de equilibrio del resorte.
LEY DE HOOKE
MOVIMIENTO ARMONICO SIMPLE
Las siguientes tres simulaciones muestran el comportamiento de un movimiento armónico simple MAS.
La simulación del centro muestra como varia la elongación (X), la velocidad (V) y la aceleración (A) del movimiento armónico simple (se puede seleccionar el periodo T del movimiento).
La Simulación de la derecha muestra como varia la energía potencia y la energía cinética del movimiento armónico simple (se puede seleccionar el periodo T del movimiento).
La forma más común de representar matemáticamente la Ley de Hooke es mediante la ecuación del muelle o resorte, donde se relaciona la fuerza ejercida en el resorte con la elongación o alargamiento producido:
F= - Kx
donde K se llama constante elástica del resorte y xes su elongación o variación que experimenta su longitud.uestra gráficamente el comportamiento del desplazamiento de las energías cinética y potenciasl de una particula que describe un Movimiento Armónico Simple.